(GER) Normalizing Flows Teil 2 - Moderne Normalizing Flows

in ML
(GER) Normalizing Flows Teil 2 - Moderne Normalizing Flows

Hier stellen wir mit modernen Flow-Architekturen wie MAF, IAF und Real-NVP Schriftzüge dar.

(Die deutsche Version beginn unten!)

This post is a follow-up on the last German post and the translation of the second post in Eric Jang’s series of posts for Normalizing Flows. I have always been involved in making content available in other languages to allow more people to enjoy it, such as when I did translations for Khan Academy. The following post is a translation of an excellent post on normalizing flows by Eric Jang, who fortunately shares my passion for making content available in different languages. So for all German-speaking folks among you - Lasst uns loslegen!

Hintergrund

In meinem letzten Post habe ich beschrieben, wie einfache Verteilungen wie Normalverteilungen “deformiert” werden können, um sie komplexen Datenverteilungen mithilfe von Normalizing Flows anzupassen. Wir haben einen einfachen Flow implementiert, indem wir 2D-Affine Bijektoren mit PreLU-Nichtlinearitäten verkettet haben, um ein kleines invertierbares neuronales Netz aufzubauen.

Dieser MLP-Flow ist jedoch ziemlich schwach: Es gibt nur 2 Einheiten pro versteckter Schicht. Außerdem ist die Nichtlinearität monoton und stückweise linear, d. h. sie führt lediglich zu einer leichten Verzerrung der Datenvielfalt um den Ursprung. Dieser Flow versagt völlig bei der Implementierung komplexerer Transformationen wie der Trennung einer isotropen Normalverteilung in zwei Modi beim Versuch, den “Two Moons”-Datensatz unten zu lernen:

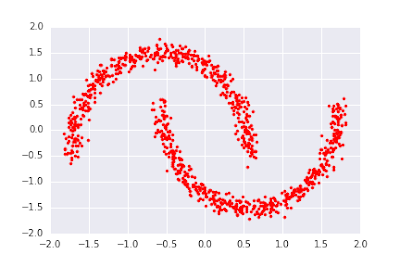
flow2_1

Glücklicherweise gibt es mehrere leistungsfähigere Normalisierungsverfahren, die in der jüngsten Literatur zum maschinellen Lernen vorgestellt wurden. In diesem Post werden wir einige dieser Techniken untersuchen.

Autoregressive Modelle sind Normalizing Flows

Autoregressive Dichteschätzverfahren wie WaveNet und PixelRNN lernen komplexe gemeinsame Dichten p(x1:D)p(x_{1:D}), indem sie die gemeinsame Dichte in ein Produkt eindimensionaler bedingter Dichten zerlegen, wobei jedes xix_i nur von den vorherigen i−1i-1 Werten abhängt: p(x)=∏ip(xi∣x1:i−1)p(x)= \prod_{i} p(x_i|x_{1:i-1})

Die bedingten Dichten haben normalerweise lernbare Parameter. Eine gängige Wahl ist zum Beispiel eine autoregressive Dichte p(x1:D)p(x_{1:D}), deren bedingte Dichte eine univariate Normalverteilung ist. Mittelwert und Standardabweichungen dieser Normalverteilung werden von neuronalen Netzen berechnet, die von den vorherigen x1:i−1x_{1:i-1} abhängen. p(xi∣x1:i−1)=N(xi∣μi,(exp⁡αi)2)p(x_i|x_{1:i-1})= \mathcal{N}(x_i | \mu_i,(\exp \alpha_i)^2) μi=fμi(x1:i−1)μ_i=f_{μ_i}(x_{1:i-1}) αi=fαi(x1:i−1)\alpha_i=f_{\alpha_i}(x_{1:i-1})

Beim Lernen von Daten mit autoregressiver Dichteschätzung wird die recht waghalsige induktive Annahme aufgestellt, dass die Variablen so sortiert sind, dass die früheren Variablen nicht von den späteren Variablen abhängen. Intuitiv sollte dies für natürliche Daten überhaupt nicht zutreffen (die oberste Pixelreihe eines Bildes hat eine kausale, bedingte Abhängigkeit vom unteren Teil des Bildes). Dennoch ist es möglich, auf diese Weise plausible Bilder zu erzeugen (zur Überraschung vieler Forscher!).

Um eine Stichprobe aus dieser Verteilung zu ziehen, berechnen wir DD “Noise-Variablen” u1:Du_{1:D} aus der Standardnormalverteilung N(0,1)\mathcal{N}(0,1) und wenden dann die folgende Rekursion an, um x1:Dx_{1:D} zu erhalten: xi=uiexp⁡αi+μix_i=u_i \exp \alpha_i+ \mu_i ui∼N(0,1)u_i \sim \mathcal{N}(0,1)

Das Verfahren der autoregressiven Stichprobenziehung (“sampling”) ist eine deterministische Transformation der zugrunde liegenden Noise-Variablen (die aus N(0,I)\mathcal{N}(0,\mathbb{I}) gezogen werden) in eine neue Verteilung, so dass autoregressives Sampling tatsächlich als eine TransformedDistribution der Standardnormalverteilung interpretiert werden kann!

Mit dieser Erkenntnis können wir mehrere autoregressive Transformationen aneinanderketten, um einen Normalizing Flow zu erhalten. Der Vorteil dieser Vorgehensweise besteht darin, dass wir die Reihenfolge der Variablen x1,...,xDx_1,...,x_D für jeden Bijektor im Flow ändern können, so dass, wenn eine autoregressive Faktorisierung eine Verteilung nicht gut modellieren kann (aufgrund einer schlechten Wahl der Variablenreihenfolge), eine nachfolgende Schicht dazu in der Lage sein könnte.

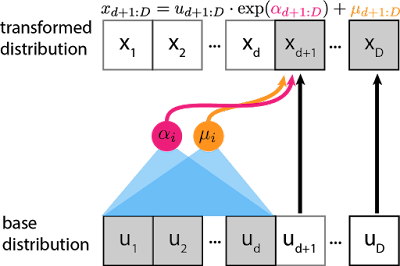
Der Masked Autoregressive Flow (MAF) Bijektor implementiert ein solches bedingt-gaußsches autoregressives Modell. Hier ein Schema des Forward-Pass für einen einzelnen Eintrag in einer Stichprobe der transformierten Verteilung, xix_i:

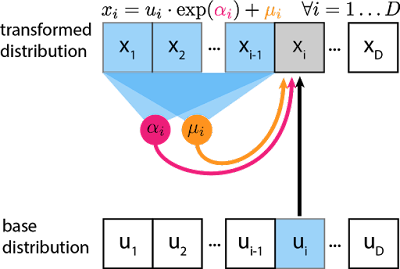
flow2_2

Der graue xix_i-Block ist die Einheit, die wir zu berechnen wollen, und die blauen Blöcke sind die Werte, von denen diese Berechnung abhängt. αi\alpha_i und μi\mu_i sind Skalare, die berechnet werden, indem x1:i−1x_{1:i-1} durch neuronale Netze geleitet wird (magenta und oranger Kreis). Auch wenn es sich bei der Transformation um eine einfache Skalierung und Verschiebung handelt, können Skalierung und Verschiebung komplexe Abhängigkeiten von früheren Variablen aufweisen. Für die erste Einheit x1x_1 werden μ\mu und α\alpha normalerweise auf lernbare skalare Variablen gesetzt, die nicht von xx oder uu abhängen.

Doch hier kommt der Knackpunkt: Die Transformation ist so konzipiert, dass die Berechnung der Inversen u=f−1(x)u=f^{-1}(x) keine Invertierung von fαf_{\alpha} oder fμf_{\mu} erfordert. Da die Transformation als Skalierung und Verschiebung parametrisiert ist, können wir die ursprünglichen Noise-Variablen durch Umkehrung der Verschiebung und Skalierung wiederherstellen: u=(x−fμ(x))/exp(fα(x))u=(x-f_{\mu}(x))/exp(f_{\alpha}(x))

Der “forward pass” und der ‘backward pass” des Bijektors hängen nur von der vorwärtsgerichteten Auswertung von fα(x)f_{\alpha}(x) und fμ(x)f_{\mu}(x) ab, so dass wir in den neuronalen Netzen fαf_{\alpha} und fαf_{\alpha} nicht invertierbare Funktionen wie ReLU und Multiplikationen mit nicht-quadratischen (=nicht invertierbaren) Matrizen verwenden können.

Der inverse Durchlauf des MAF-Modells wird zur Berechnung der Dichte verwendet:

distribution.log_prob(bijector.inverse(x)) + bijector.inverse_log_det_jacobian(x))

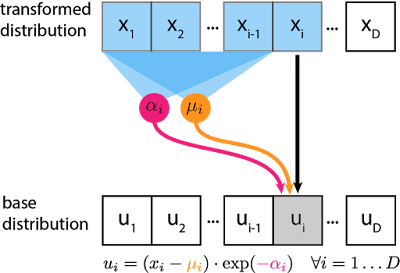
flow2_3

Laufzeit-Komplexität und MADE

Autoregressive Modelle und MAF können “schnell” trainiert werden, da alle bedingten Wahrscheinlichkeiten p(x1),p(x2∣x1),...p(xD∣x1:D−1)p(x_1),p(x_2 \mid x_1),...p(x_D \mid x_{1:D-1}) in einem einzigen Durchlauf von DD Threads gleichzeitig ausgewertet werden können, wobei die Parallelität moderner GPUs genutzt wird. Wir gehen davon aus, dass Parallelität, wie z. B. SIMD-Vektorisierung auf CPUs/GPUs, keinen Laufzeit-Overhead hat.

Andererseits ist das Sampling autoregressiver Modelle langsam, weil man warten muss, bis alle vorherigen x1:i−1x_{1:i-1} berechnet sind, bevor man neue xix_i berechnet. Die Laufzeitkomplexität der Erzeugung einer einzelnen Stichprobe besteht aus D sequentiellen Durchläufen eines einzelnen Threads, wodurch die Parallelität der Prozessoren nicht genutzt wird.

Ein weiteres Problem: Sollten wir im parallelisierbaren inversen Durchlauf separate neuronale Netze (mit unterschiedlich großem Input) für die Berechnung von jedem αi\alpha_i und μi\mu_i verwenden? Das ist ineffizient, insbesondere wenn man bedenkt, dass die gelernten Repräsentationen zwischen diesen D Netzwerken gemeinsam genutzt werden sollten (solange die autoregressive Abhängigkeit nicht verletzt wird). In dem Paper Masked Autoencoder for Distribution Estimation (MADE) schlagen die Autoren eine sehr schöne Lösung vor: Verwendung eines einzigen neuronalen Netzes zur gleichzeitigen Ausgabe aller Werte von α\alpha und μ\mu, aber Maskierung der Gewichte, damit die autoregressive Eigenschaft erhalten bleibt.

Mit diesem Trick ist es möglich, alle Werte von uu aus allen Werten von xx mit einem einzigen Durchlauf durch ein einziges neuronales Netz (D Inputs, D Outputs) zu ermitteln. Dies ist wesentlich effizienter als die gleichzeitige Verarbeitung von D neuronalen Netzen (D(D+1)/2 Inputs, D Outputs).

Zusammenfassend lässt sich sagen, dass MAF die MADE-Architektur als Effizienztrick für die Berechnung nichtlinearer Parameter von Shift-and-Scale-autoregressiven Transformationen nutzt und diese effizienten autoregressiven Modelle in das Normalizing Flow Konzept integriert.

Inverser Autoregressiver Flow (IAF)

Beim inversen autoregressiven Flow werden die nichtlinearen Verschiebungs-/Skalierungsstatistiken unter Verwendung der vorherigen Noise-Variablen u1:i−1u_{1:i-1} anstelle der Datenpunkte x1:i−1x_{1:i-1} berechnet: xi=uiexp⁡αi+μix_i = u_i \exp \alpha_i + \mu_i μi=fμi(u1:i−1)\mu_i = f_{\mu_i}(u_{1:i-1}) αi=fαi(u1:i−1)\alpha_i = f_{\alpha_i}(u_{1:i-1})

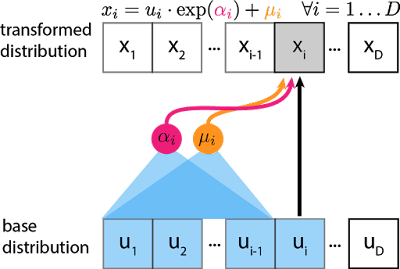
flow2_4

Der “forward pass” (sampling) von IAF ist schnell: alle xix_i können in einem einzigen Durchlauf von D parallel arbeitenden Threads berechnet werden. IAF verwendet auch MADE-Netzwerke, um diese Parallelität effizient zu implementieren.

Wenn wir jedoch einen neuen Datenpunkt erhalten und die Dichte auswerten sollen, müssen wir uu wiederherstellen, und dieser Prozess ist langsam: zuerst berechnen wir u1=(x−μ1)exp⁡(−α1)u_1=(x-μ_1) \exp(-\alpha_1), dann führen wir dies sequentiell fort: ui=(x−μi(μ1:i−1))exp⁡(−αi(u1:i−1))u_i=(x-μ_i(\mu_{1:i-1})) \exp(-\alpha_i(u_{1:i-1}))

Andererseits ist es trivial, die (logarithmische) Wahrscheinlichkeit der durch IAF erzeugten Stichproben zu verfolgen, da wir bereits alle uu-Werte kennen, ohne von xx aus invertieren zu müssen.

Dem aufmerksamen Leser wird auffallen, dass, wenn man die untere Reihe als x1,...xDx_1, ... x_D und die obere Reihe als u1,...uDu_1, ... u_D bezeichnet, dies genau dem inversen Pass des MAF-Bijektors entspricht! Ebenso ist die Inverse von IAF nichts anderes als der Vorwärtspass von MAF (mit vertauschten xx und uu). Daher sind MAF und IAF in TensorFlow Distributions tatsächlich mit der gleichen Bijector-Klasse implementiert, und es gibt eine bequeme “Invert”-Funktion für die Invertierung von Bijektoren, um ihre inversen und vorwärts gerichteten Durchläufe zu vertauschen.

iaf_bijector = tfb.Invert(maf_bijector)

IAF und MAF bieten entgegengesetzte Kompromisse bei der Berechnung - MAF trainiert schnell, aber mit langsamen Stichproben, während IAF langsam trainiert, aber mit schnellen Stichproben. Für das Training neuronaler Netze benötigen wir in der Regel viel mehr Durchsatz bei der Dichteauswertung als beim Sampling, so dass MAF in der Regel die bessere Wahl beim Lernen von Verteilungen ist.

Parallel Wavenet

Eine naheliegende Folgefrage ist, ob diese beiden Ansätze kombiniert werden können, um das Beste aus beiden Welten zu erhalten, d.h. schnelles Training und Sampling.

Die Antwort lautet: Ja! Das oft erwähnte Parallel Wavenet von DeepMind macht genau das: ein autoregressives Modell (MAF) wird verwendet, um ein generatives Modell effizient zu trainieren; dann wird ein IAF-Modell trainiert, um die Likelihood seiner eigenen Stichproben unter diesem Lehrer zu maximieren. Es sei daran erinnert, dass es bei IAF kostspielig ist, die Dichte externer Datenpunkte (z. B. aus dem Trainingsdatensatz) zu berechnen, aber es kann die Dichte seiner eigenen Stichproben kostengünstig berechnen, indem es die Noise-Variablen u1:Du_{1:D} zwischenspeichert und so den “inverse pass” nicht aufrufen muss. Auf diese Weise können wir das “Schüler”-IAF-Modell trainieren, indem wir die Divergenz zwischen der Schüler- und der Lehrer-Verteilung minimieren.

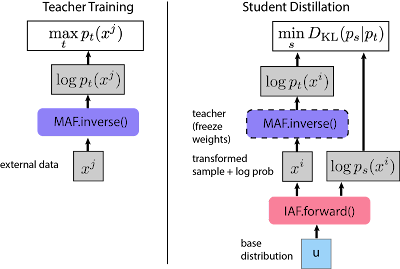
flow2_5

Dies ist eine Anwendung von Forschung über Normalizing Flows, die sehr große Auswirkunge hat - das Endergebnis ist ein Echtzeit-Audiosynthesemodell, das 20 Mal schneller samplen kann und bereits in realen Produkten wie dem Google Assistant eingesetzt wird.

NICE und Real-NVP

Zum Schluss betrachten wir das Real-NVP, das als Spezialfall des IAF-Bijektors angesehen werden kann.

In einer NVP-“Kopplungsschicht” legen wir eine ganze Zahl 0<d<D0<d<D fest. Wie bei IAF ist xd+1x_{d+1} eine Verschiebung und Skalierung, die von früheren udu_d-Werten abhängt. Der Unterschied besteht darin, dass wir auch xd+2,xd+3,...xDx_{d+2}, x_{d+3},...x_D dazu zwingen, nur von diesen udu_d-Werten abzuhängen, so dass ein einziger Durchlauf durch das Netzwerk verwendet werden kann, um αd+1:D\alpha_{d+1:D} und μd+1:D\mu_{d+1:D} zu erzeugen.

Bei x1:dx_{1:d} handelt es sich um “Pass-Through”-Einheiten, d.h. sie werden gleichgesetztt zu u1:du_{1:d}. Daher ist Real-NVP auch ein Spezialfall des MAF-Bijektors (da α(u1:d)=α(x1:d)\alpha(u_{1:d})=\alpha(x_{1:d})).

flow2_6

Da die Verschiebungs- und Skalierstatistiken für die gesamte Schicht entweder aus x1:dx_{1:d} oder u1:du_{1:d} in einem einzigen Durchgang berechnet werden können, kann NVP die Vorwärts- und Rückwärtsberechnungen in einem einzigen parallelen Durchgang durchführen (Sampling und Dichteschätzung sind beide schnell). MADE ist ebenfalls nicht erforderlich.

Empirische Studien deuten jedoch darauf hin, dass Real-NVP tendenziell schlechter abschneidet als MAF und IAF, und ich habe die Erfahrung gemacht, dass NVP meine 2D-Toy-Datensätze (z. B. den SIGGRAPH-Datensatz) bei Verwendung der gleichen Anzahl von Schichten schlechter anpasst. Real-NVP und IAF sind im 2D-Fall nahezu äquivalent, außer dass die erste Einheit von IAF weiterhin durch eine Skalierung und Verschiebung transformiert wird, die nicht von u1u1 abhängt, während Real-NVP die erste Einheit unverändert lässt.

Real-NVP war eine Folgearbeit des NICE-Bijektors, einer reinen Verschiebungsvariante, die α=0\alpha=0 annimmt. Da NICE die Verteilung nicht skaliert, ist die ILDJ tatsächlich konstant!

Batch-Normalisierungs-Bijektor

Das Real-NVP-Papier schlägt mehrere neue Beiträge vor, von denen einer ein Batch-Normalisierungs-Bijektor ist, der zur Stabilisierung des Trainings verwendet wird. Konventionell wird die Batch-Norm auf das Training neuronaler Netze angewandt, wobei die Vorwärtsstatistiken mittelwertzentriert und auf eine diagonale Einheitskovarianz skaliert sind und die Batch-Norm-Statistiken (gleitender Mittelwert, gleitende Varianz) über einen exponentiellen gleitenden Durchschnitt akkumuliert werden. Zum Testzeitpunkt werden die akkumulierten Statistiken zur Normalisierung der Daten verwendet.

Bei der Normalisierung der Datenflüsse wird die Batch-Norm in bijector.inverse während des Trainings verwendet, und die akkumulierten Statistiken werden zur De-Normalisierung der Daten zur “Testzeit” (bijector.forward) verwendet. Konkret werden BatchNorm-Bijektoren in der Regel wie folgt implementiert:

  • Inverse Pass:
    1. Berechne den aktuellen Mittelwert und die Standardabweichung der Datenverteilung x.
    2. Aktualisiere den gleitenden Mittelwert und die gleitende Standardabweichung
    3. Normalisiere die Daten mit Batch-Norm anhand des aktuellen Mittelwerts/der aktuellen Standardabweichung
  • Forward Pass:
    1. Verwende den gleitenden Mittelwert und die Standardabweichung zur Entnormalisierung der Datenverteilung.

Dank TF Bijectors kann dies mit nur wenigen Zeilen Code umgesetzt werden:

# file: "nf2_batchnorm.py"
class BatchNorm(tfb.Bijector):
    def __init__(self, eps=1e-5, decay=0.95, validate_args=False, name="batch_norm"):
        super(BatchNorm, self).__init__(
            event_ndims=1, validate_args=validate_args, name=name)
        self._vars_created = False
        self.eps = eps
        self.decay = decay

    def _create_vars(self, x):
        n = x.get_shape().as_list()[1]
        with tf.variable_scope(self.name):
            self.beta = tf.get_variable('beta', [1, n], dtype=DTYPE)
            self.gamma = tf.get_variable('gamma', [1, n], dtype=DTYPE)
            self.train_m = tf.get_variable(
                'mean', [1, n], dtype=DTYPE, trainable=False)
            self.train_v = tf.get_variable(
                'var', [1, n], dtype=DTYPE, initializer=tf.ones_initializer, trainable=False)
        self._vars_created = True

    def _forward(self, u):
        if not self._vars_created:
            self._create_vars(u)
        return (u - self.beta) * tf.exp(-self.gamma) * tf.sqrt(self.train_v + self.eps) + self.train_m

    def _inverse(self, x):
        # Eq 22. Called during training of a normalizing flow.
        if not self._vars_created:
            self._create_vars(x)
        # statistics of current minibatch
        m, v = tf.nn.moments(x, axes=[0], keep_dims=True)
        # update train statistics via exponential moving average
        update_train_m = tf.assign_sub(
            self.train_m, self.decay * (self.train_m - m))
        update_train_v = tf.assign_sub(
            self.train_v, self.decay * (self.train_v - v))
        # normalize using current minibatch statistics, followed by BN scale and shift
        with tf.control_dependencies([update_train_m, update_train_v]):
            return (x - m) * 1. / tf.sqrt(v + self.eps) * tf.exp(self.gamma) + self.beta

    def _inverse_log_det_jacobian(self, x):
        # at training time, the log_det_jacobian is computed from statistics of the
        # current minibatch.
        if not self._vars_created:
            self._create_vars(x)
        _, v = tf.nn.moments(x, axes=[0], keep_dims=True)
        abs_log_det_J_inv = tf.reduce_sum(
            self.gamma - .5 * tf.log(v + self.eps))
        return abs_log_det_J_inv

Die ILDJ lässt sich leicht ableiten, indem man einfach die logarithmische Ableitung der inversen Funktion nimmt (wie beim univariaten Fall).

Code Beispiel

Dank der Bemühungen von Josh Dillon und dem Google Bayesflow-Team gibt es bereits eine flexible Implementierung des MaskedAutoregressiveFlow Bijektors, die MADE-Netzwerke zur Implementierung einer effizienten Wiederherstellung von uu für das Training verwendet.

Ich habe mit diesem Blender-Skript eine komplexe 2D-Verteilung erstellt, die eine Punktwolke in Form der Buchstaben “SIGGRAPH” ist. Wir konstruieren unseren Datensatz, den Bijektor und die transformierte Verteilung auf eine sehr ähnliche Weise wie im ersten Tutorial, daher werde ich die Codeblöcke hier nicht wiederholen - das Jupyter-Notebook findet ihr hier. Dieses Notebook kann einen Normalisierungsfluss mit MAF, IAF, Real-NVP mit/ohne BatchNorm für die Datensätze “Two Moons” und “SIGGRAPH” trainieren.

Ein Detail, das leicht übersehen werden kann, ist, dass dies überhaupt nicht funktioniert, es sei denn man ändert die Reihenfolge der Variablen nach jedem Flow. Andernfalls wird keine der autoregressiven Faktorisierungen der Schichten die Struktur von p(x1∣x2)p(x_1 \mid x_2) lernen. Glücklicherweise hat TensorFlow einen Permute-Bijektor, der speziell für diese Aufgabe entwickelt wurde.

# file: "nf2_chain.py"
for i in range(num_bijectors):
    bijectors.append(tfb.MaskedAutoregressiveFlow(
      shift_and_log_scale_fn=tfb.masked_autoregressive_default_template(
      hidden_layers=[512, 512])))
    bijectors.append(tfb.Permute(permutation=[1, 0]))
flow_bijector = tfb.Chain(list(reversed(bijectors[:-1])))

Hier ist der gelernte Flow, zusammen mit dem Endresultat. Es erinnert mich ziemlich an eine Taffy-Machine.

flow2_7

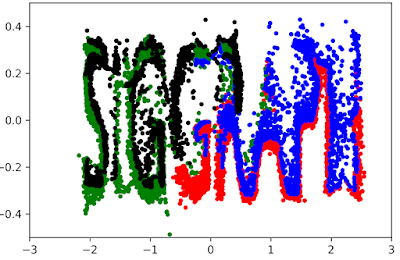
flow2_8

Diskussion

TensorFlow-Verteilungen vereinfachen die Implementierung von Normalizing Flows und akkumulieren automatisch alle Jacobi-Determinanten in einer Kette für uns in einer Weise, die sauber und gut lesbar ist. Bei der Entscheidung, welchen Normalizing Flow man benutzt, sollte man die Balance zwischen einem schnellen forward pass und einem schnellen inverse pass im Kopf behalten. Zusätzlich sollte man bedenken, wie ausdrucksstark der Flow und wie schnell die ILDJ ist.

In Teil 1 des Tutorials habe ich Normalizing Flows damit motiviert, dass wir leistungsfähigere Verteilungen benötigen, die beim Reinforcement Learning und der generativen Modellierung eingesetzt werden können. Im Großen und Ganzen ist es nicht klar, ob die volumenverfolgenden Normalizing FLows tatsächlich das beste Werkzeug für AI-Anwendungen wie Robotik und strukturierte Vorhersage sind, wenn Techniken wie Variationsinferenz und implizite Dichtemodelle in der Praxis bereits sehr gut funktionieren. Dennoch sind Normalizing Flows eine nette Familie von Methoden, die man in der Tasche haben sollte, und sie haben nachweislich reale Anwendungen, wie z. B. in generativen Audiomodellen in Echtzeit, die in Google Assistant eingesetzt werden.

Obwohl Modelle mit expliziter Dichte wie Normalizing Flows für Maximum-Likelihood-Training geeignet sind, ist dies nicht die einzige Möglichkeit, wie sie verwendet werden können, und sie sind eine Ergänzung zu VAEs und GANs. Es ist möglich, Normalizing Flows als direkten Ersatz für Normalverteilungen zu verwenden, z. B. für VAE-Priors und latente Variablen in GANs. Zum Beispiel verwendet dieses Paper Normalizing Flows als flexible Variational Priors, und das Paper über TensorFlow-Verteilungen stellt einen VAE vor, der einen Normalizing Flow als Prior zusammen mit einem PixelCNN-Decoder verwendet. Parallel Wavenet trainiert ein IAF-“Studenten”-Modell über KL-Divergenz.

Eine der faszinierendsten Eigenschaften von Normalizing Flows ist, dass sie eine reversible Berechnung implementieren (d.h. eine definierte Inverse einer ausdrucksstarken Funktion haben). Das bedeutet, dass wir, wenn wir einen Backprop-Durchgang durchführen wollen, die Vorwärtsaktivierungswerte neu berechnen können, ohne sie während des Vorwärtsdurchgangs im Speicher speichern zu müssen (was bei großen Graphen potenziell teuer ist). In einer Situation, in der das “Credit Assignment” über sehr lange Zeiträume hinweg erfolgen kann, können wir die reversible Berechnung nutzen, um vergangene Entscheidungszustände “wiederherzustellen” und dabei den Speicherbedarf in Grenzen zu halten. Diese Idee wurde bereits im RevNets-Paper verwendet und wurde durch die Invertierbarkeit des NICE-Bijektors inspiriert. Das erinnert mich an die Hauptfigur aus dem Film Memento, die nicht in der Lage ist, Erinnerungen zu speichern, und deshalb invertierbare Berechnungen verwendet, um sich an Dinge zu erinnern.

Vielen Dank fürs Lesen!

Credits

Wie beim ersten Teil schon vielen Dank an Eric Jang für die Möglichkeit, dieses coole Tutorial mehr Leuten zugänglich zu machen!

Weiteres Material

Photo by JJ Ying on Unsplash